Óraparadoxon
A sebesség hatására megnő a test tömege, valamint az atomórák ritmusa lelassul. Az 1971-es Hafele kísérlet ezt közel bebizonyította. Legfőbb tanulsága azonban, hogy a sebesség valójában abszolút, nem pedig relatív !

Bő évszázada született meg az a hipotézis, mely szerint a sebesség hatására az órák késnek. Később a fizikusok atomóra kísérlettel próbálták ellenőrizni e szokatlan - bátran mondhatjuk, hogy paradox - állítást, melyet azután az eredmények részben igazoltak, részben cáfoltak. A jelenséget leíró számítások helyessége és pontossága mindmáig kétséges és vitatott. Bár a többség a relativitáselméletre alapoz, e dolgozatban megmutatjuk, hogy ez a kiinduló alap itt sem elméletileg, sem gyakorlatilag nem használható. Helyette a klasszikus mechanika egyenletei szolgáltatják a korrekt, és ugyanakkor szemléletes megoldást. A jelenség hátterének feltárásához szükség volt két további felismerésre is.
A levezetett új formula részben eltérő, részben komplexebb, mint a régi. Kimunkálásra került néhány további atomórás kísérlet is, melyektől jól körülhatárolt, és egyúttal pontosabb eredményeket várhatunk. Ezeknél az új formula jóslatai jelentősen eltérnek a korábbitól, megkönnyítve ezzel a választást a kétféle elmélet és a kétféle formula között. Ugyanakkor ezek a kísérletek tisztázzák a vonatkozó geometriai viszonyokat, valamint oszlatják a témakörre tapadt tévhiteket. Az új elmélet talaján állva és onnan körbepillantva számos merőben újszerű fizikai entitással találjuk szembe magunkat, melyekből néhányra ebben a dolgozatban is kitérünk.
Régen, még a XIX. században vált közérdeklődés tárgyává egy optikai kísérlet, mert ennek eredménye szöges ellentétben állt az elvárásokkal, illetve a kor fizikai világképével. Az un. M-M kísérletből a fizikusok arra következtettek, hogy nincs éter, vagy pedig a fény mind az álló, mind a mozgó tárgyak mellett egyazon c sebességgel halad el. Esetleg a sebesség hatására megváltozik az idő ritmusa, az órák lassabban járnak. Einstein még diákként találkozott e feltevésekkel, elfogadta azokat, és manapság már - tévesen - neki tulajdonítják az alapötletet.
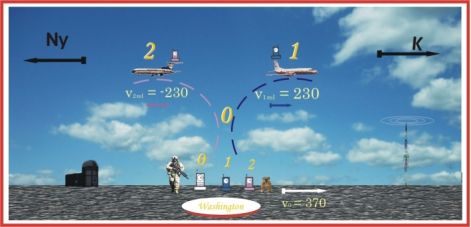
A feltevés kísérleti ellenőrzése csak jóval később, az atomóra megszületése után vált lehetővé. A kísérletre 1971-ben került sor. Egy fizikus és egy csillagász - Hafele és Keating - Washingtonban felült egy utasszállító gépre, hogy körülrepülje a Földet. Négy [*] atomórát vittek magukkal. Mintegy 2 napot repültek keleti irányban, és visszaérve az órák átlag 59 nano-szekundumot késtek. A második Föld-kerülés nyugati irányban történt, amely viszont +273 ns óra-sietést eredményezett.
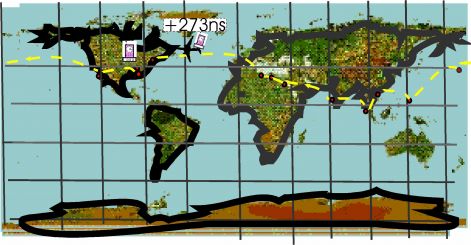
Tekintsük a fenti két eredményt a magasság és a sebesség, illetve a helyzeti és a mozgási energia hatásának. E feltételezés igen kézenfekvő, és látni fogjuk, hogy a számítás is meggyőzően alátámasztja.
A repülés velejárója a magasság növekedése, melynek következtében a cézium atomóra ritmusa gyorsul. A számítás menete a következő:
(Aki a számításokat nem kedveli, annak talán érdemes átmennie a másik honlapomra. Ott egy könnyített változat szerepel.)
A helyzeti energia változása (1. képlet):
![]()
A tömeg növekedése az E=mc2 összefüggést használva (2. képlet):
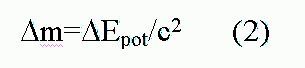
Az óra sietése - így logikus és a kísérlet ezt igazolja vissza - a tömegnövekedéssel és a magasban tartózkodás időtartamával arányos. A próbatömeg egységnyi, m=1 (3. képlet) : [**]
![]()
ahol M a Föld tömege, G a gravitációs állandó,
R1 a repülőgép távolsága a Föld középpontjától, R3 a repülőtéren hagyott óra távolsága a Föld középpontjától.
A sebesség az atomóra lassulását okozza. Ha nem lenne más befolyásoló tényező, akkor az óra késését az alábbi egyszerű lépések mentén számíthatnánk ki:
A mozgási energia (4. képlet):
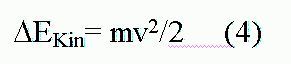
A tömeg növekedése (5. képlet):
![]()
Az óra késése (6. képlet):
![]()
Bonyolítja a helyzetet, hogy a Föld forog, ezért felszínének (és légkörének) számottevő kerületi sebessége van. Nagysága a Föld forgástengelyétől mért távolsággal arányos. Nevezhetjük rejtőző sebességnek is, mivel jelenlétét igen nehéz felismerni ill. tudatosítani.
A rejtőző sebesség számítása (7. képlet):
![]()
ahol R1 a Föld középpontjából a repülőgépre mutató vektor, W a Föld szögsebesség vektora, Q1 szögérték, a repülés szélességi köre.
Azonban a kísérletben nem csak a repülőgépnek volt rejtőző sebessége, hanem a földön maradt referencia órának is (8. képlet):
![]()
ahol R3 a referencia óra távolsága a Föld középpontjától, W a Föld szögsebessége, Q3 szögérték a referencia óra szélességi köre.
Ezen v3 sebesség felbukkanása után kényszerűen megváltozik a Washingtonban hagyott óráról alkotott prekoncepciónk. Ez az óra nem állt, nem alapállapotban volt, hanem tekintélyes, cca. 370 m/s sebességgel száguldott keleti irányba. E rejtőző sebesség nyilván lecsökkentette a cézium atomok által kisugárzott alapjel frekvenciáját. Megtévesztő lehet, hogy az óra számlapja ennek ellenére a pontos időt (a csillagászati időt) mutatta. Ezt a kedvező állapotot még jóval korábban érték el, mégpedig a közbülső elektronika (digitális frekvenciaosztó) kézi állítgatásával, beszabályozásával. Az utazó órák szinkronizálása ugyanott (egyazon földrajzi ponton), tehát egyazon rejtőző sebesség befolyása alatt történt. A módosult kezdő állapot hatása maradandó volt, mert a hozzáadott sebesség nem lineáris, hanem négyzetes változást okoz.
Nem csak a repülés befolyásolja az órát. Egy másik szélességi körön - például egy másik repülőtéren - más a rejtőző sebesség nagysága, és ettől is megváltozik az óra ritmusa. A számításnak tehát a kísérlet teljes időtartamára (Ttotal) ki kell terjednie.
A fenti meggondolások alapján a 3 féle sebesség hatása az utazó órára a következő (9. képlet):
![]()
Ugyanez a képlet skalár változatban (10. képlet):
![]()
ahol v1 a repülőgép sebessége, l a repülés irányszöge (Észak 0°, Kelet 90° stb.), Dt azon időintervallum, melyben a paramétereket változatlanoknak tekintjük. R1, W, Q1, R3, Q3 paraméterek értelmezését a (7) és (8) képleteknél adtuk meg.
A tárgyi kísérletben az atomórák a magasság és a sebesség együttes hatását jelezték ki, ezért a (10) képletet ki kell egészítenünk a gravitációs (3) képlettel, majd summázunk kell a Dt időintervallumokat a teljes (Ttotal) kísérleti időtartamra. Az atomóra sietése/késése tehát (11. képlet):
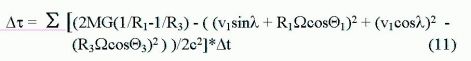
E formula alkalmas lenne arra, hogy elegendő adat birtokában Dt értékét korrekt módon kiszámítsuk. Azonban a kutatók nem publikálták a begyűjtött 125 ill. 108 időintervallum részadatait. Cikkükben [1],[2]csupán néhány átlagértéket adtak meg. Ezek: az aktív repülési idő (Tflight), teljes kísérleti idő (Ttotal), és az átlagos magasság. Hozzáférhető információ még a repülési sebesség és az utazás közbülső repülőterei, melynek alapján megbecsülhető az út hossza. (1 táblázat) Rendelkezésre állnak még Hafele számításának részeredményei: a gravitációból és a sebességből általa számított időcsúszások. (Lásd 2. Táblázat.) Mindezek együtt is csak egy hiányos, heterogén, korrekt számításra alkalmatlan adathalmazt alkotnak. A számítás rekonstruálása végül is sikerrel járt a (11) formula segítségével. E számítás során természetesen Hafele részeredményeit kaptuk vissza. (Lásd 3. Táblázat.) A számítási folyamat során nyert Q1 értékek azonban lehetőséget adtak a kétféle számítás összevetésére azonos input adatok mellett. Az eltérés 8% volt.
Hafele eredeti képlete [1] (12. képlet):
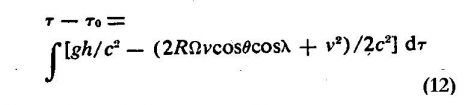
Első pillantásra látszik, hogy ez a képlet kevesebb tagot tartalmaz, így eleve nem érheti el a korrekt (11) formula pontosságát. (Lásd 3. Táblázat.) Hafele képlete tehát elviekben is és a gyakorlatban is hibás. Érdemes sorra venni a hibákat(h) a kísérlet helyes értelmezése érdekében:
Az integrálás használata itt nem jogos, hiszen nem végtelenül kicsiny, hanem nagyméretű szakaszokat kellett összegezni (h1). A repülés irányszöge (l) a szokásostól eltérő, amennyiben az északi irányt a 270° jelöli (h2). A képlet első, gravitációs tagja nem elég általános, nagyobb h értékeknél (pl. műholdak esetében) pontatlan (h3). A képlet 2. tagja értelemszerű sorrendben írva: 2RWcosQ*vcosl (h4). Világosan látszik, hogy Hafele nem érti az összefüggéseket, továbbá az alkalmazott elmélet alkalmatlan a probléma megoldására (h4). (Az eddig felsorolt apró hibák csupán zavaró tényezők, és nem okoztak számszerű eltérést a végeredményben.) Hiányzik (az itt nem idézett) (9) képletben szereplő v12 és v32 tag. Ezek a repülőgép névleges sebességét és a referencia óra rejtőző sebességét jelentik. Általában ezek különböző értékek, ezért kivonással nem válnak 0-vá, tehát elhagyásuk nem jogos (h5). Ugyanakkor a képletben a 3. tag v2, míg ez helyesen a (v1sinl)2 lenne, azaz a névleges sebesség észak-dél irányú komponensének négyzete (h6). Hafele a repüléssel töltött Tflight időtartammal számolt a két óraegyeztetés között eltelt teljes Ttotal időtartam helyett. Ezáltal elveszett az eltérő magasságú és szélességi körű repülőtereken töltött idő hatása(h7). A Szerzők hangsúlyozottan az SR és GR elméletek alapján kívánták a paradoxont megoldani. A (12) képlet a bizonyíték rá, hogy ez minden erőfeszítésük ellenére sem sikerült (h8). Az elvi hibák mellett a formula a gyakorlati számolás során is túllépte az elfogadható hibahatárt. Még jelentősebb hibát mutatott volna Hafele képlete, ha a földkerülés nem Washington szélességi körén, hanem az Egyenlítőn történt volna(h9).
Dr. Alphonsus G. Kelly ír fizikus az elvégzett kísérletek színvonalát kritizálta. Internetes tanulmányaiban hosszan részletezte, hogy Hafele hányszor állítgatta át az órákat, miért volt kénytelen eltitkolni a részeredményeket stb. Ezek alapján jogosan állította, hogy a kísérlet a legelemibb tudományos követelményeket sem elégítette ki.
Nyílván Hafele sem jókedvében hágta át a szabályokat. Két lehetősége volt.Az egyik, hogy bejelenti, hogy a kísérlet sikertelen, mert a Washingtoni Időközponttól kölcsön kapott atomórák amúgy is gyenge minőségűek voltak, ráadásul rosszul bírták az utasszállító gépek vibrációját. A másik - a megvalósított - lehetőség, hogy jó eredményeket "generál", hiszen előre kiszámolta, hogy mit kell felmutatnia. A kísérlet akkoriban elméleti oldalról igen nagy jelentőséggel bírt (és bír manapság is), a tudományos közösség már nagyon szeretett volna átbillenni a holtponton. Ezért aztán a több mint gyanús publikációkat lelkesen fogadták, a kísérletezőket megdicsérték. Az élenjáró tudományos lapok leközölt cikkei maguk is nagy kitüntetést jelentenek egy kutató számára [1], [2]. Sőt, az a kivételes eset is megesett, hogy a Nature főszerkesztője is méltató cikket írt Hafeléék teljesítményéről [3]. Nem véletlen tehát, hogy a tudományos körök elengedték a fülük mellett Kelly jogos kritikáit.
Fontos leszögezni, hogy az újabb- és újabb kísérletek mind megerősítették Hafele kísérleti eredményként feltálalt hipotézisét.
Magasabb tudományos kitűntetést is kaphatott volna a H-K páros, ha sikerül világos és pontos eredményt szolgáltató elméletet tenniük a híres kísérlet mögé. A helyes elméletet a klasszikus mechanika egyszerű törvényei szolgáltatják, melyeket a fentiekben ismertettem nagy vonalakban.
A H-K kísérlet számos elméleti problémát hozott felszínre. Ezek tisztázása, pontosítása és a perspektíva szélesítése érdekében 3 tényleges kísérletet javaslok elvégezni. Ezek az eredeti kísérletnél pontosabb eredményt ígérnek kisebb költség mellett. Továbbá megfelelnek annak az alapvető elvárásnak, mely szerint egy adott kísérlet során csak egyetlen paramétert szabad változtatni. (A H-K kísérletben sajnos 2 paraméter is változott; a magasság és a sebesség.)
1. kísérlet: A magasság hatása
Vigyünk fel egy atomórát egy 4 km magas hegy csúcsára, míg a referencia-órát tegyük a hegy lábához. A felső óra 10 nap alatt 377 ns-t fog sietni, mind a (11), mind a (12) képlet jóslata szerint.
2. kísérlet: Atomóra az Egyenlítőn
Vegyünk egy Washingtonban beszabályozott órát és helyezzük le az Egyenlítőre. A 10 napos időintervallum kezdetét és végét rádió-impulzusok jelezzék. A (11) formula szerint az óra -383 ns késést fog mutatni, ami az ottani nagyobb (464 m/s) rejtőző sebesség következménye. Hafele (12) képlete ezzel szemben 0 változást mond.
3. kísérlet: Atomóra a Póluson
Vegyünk egy Washingtonban beszabályozott órát és helyezzük le az Északi pólusra (vagy egy ehhez közeli szárazföldre). A 10 napos időintervallum kezdetét és végét itt is rádió-impulzusok szolgáltatják. A (11) formula szerint az óra +651 ns sietést fog mutatni, ami az ottani kisebb (valójában 0) rejtőző sebesség következménye lesz. Hafele (12) képlete ezzel szemben 0 változást mond. A következőkben további három gondolatkísérlet kerül ismertetésre, melyek célja leginkább a problémakör geometriájának részletesebb megismerése. E kísérleteket egyrészt nehéz lenne elvégezni, másrészt nem szolgálnak többlet-információval.
4. kísérlet: Földkerülés egy poláris műhold síkjában
A poláris műhold olyan síkban kering, amely a Föld pólusain fekszik és térbeli irányát nem változtatja. Úgy vehetjük, hogy a Föld ezen síkhoz képest forog. A repülőgép e síkban, közel tengerszint magasságban kerüli meg a földgolyót egy utasszállító gép átlagos, 230 m/s -os sebességével. (Tekintsünk el a hegyektől, és a magasföldektől.) Mindkét egyenlet a repülő óra -51 ns késését jósolja egy Póluson hagyott referencia-órához képest. Egy a Földdel együttmozgó távolabbi helyről, például a Holdról nézve a gép pályája egyszerű kör (vetületben ellipszis). Ugyanakkor az Egyenlítőn álló megfigyelő olyan repülőgépet lát, amely 518 m/s szuperszonikus sebességgel száguld el a fejje fölött Ny-ÉNy irányában (l=296 fok).
5. kísérlet: Földkerülés hosszúsági körön
A Déli pólustól az Északi pólusig repülünk, majd a túloldalon vissza. Ez egyszerű körpályának tűnik egy földi megfigyelő számára. A Holdról nézve ugyanezt egy Földre csavarodott kígyóvonalnak látnánk, és ez utóbbi a valóság. Például amikor a repülőgép az Egyenlítő fölött jár, akkor északi irányú sebessége ugyan 230 m/s, de közben keleti irányú (rejtőző) sebessége 464 m/s. E helyzettel összhangban a (11) képlet nagy értékű óra-késést jósol, -310 ns-t. A Hafele képlet ez esetben is csak -51 ns-t mond.
6. kísérlet: Repülés nyugatnak
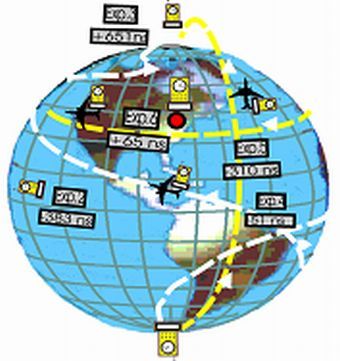
Washington repülőteréről nyugatnak startolva állítsunk egy szuperszonikus repülőgépet földkerülő pályára. Növelve a gép sebességet a fedélzeten elhelyezett atomóra ritmusa gyorsulni fog, ahogyan ezt a H-K kísérlet is mutatta. Amikor a gép eléri az alatta elterülő földfelszín rejtőző sebességét (370 m/s), akkor jár az óra a lehető leggyorsabban. (Ha még tovább növelnénk a gép sebességét, akkor az óra újra lassabban kezdeni járni.) Egy nap alatt megkerülve a Földet az óra sietése +65 ns lesz mindkét képlet szerint. A hátra lévő három kísérletet már korábban lefolytatták, bár esetenként egész más céllal. Elegendő tehát az eredményeket utólag kielemezni.
7. kísérlet: GPS műholdak
E holdak pályája úgy van kiszámítva, hogy naponta kétszer kerülik meg a Földet 20400 km magasságban. Pályájuk 55 fokos szöget zár be az Egyenlítő síkjával. A bennük lévő atomórát még fellövés előtt alacsonyabb ritmusra állítják, mert odafönt az óra napi 39 mikro-szekundumot (ms) siet. A (11) formula erre 38,6 ms-t jósol. Hafele képlete torz eredményt add 182 ms-t. Ezen belül a képlet sebességi része is jelentős, 15%-nyi hibát eredményez.
8. kísérlet: A Föld pályasebességének hatása
A Föld igen tekintélyes, cca. 30 000 m/s sebességgel kering a Nap körül. Ehhez éjjel hozzáadódik Washington kerületi sebessége, nappal kivonódik, így azt várnánk, hogy az atomórák ritmusa a napszakok szerint változik. Ennek értéke a (11) formula alapján számolva 6819 ns lenne. Más hosszúsági körön üzemelő atomóráknál az időcsúszás más-más fázisban jelentkezne. Efféle ingadozást azonban nem észleltek, ami azt jelenti, hogy a Föld pályasebessége egyáltalán nem jut el a felszíni tárgyakig.
9. kísérlet: Egyenes szakaszokból körpálya
Gyakran lehet találkozni azzal a vélekedéssel, hogy a H-K kísérlet - a földkerülés - lényegileg körmozgás, melyre másmilyen fizikai törvények vonatkoznak. A vitát elkerülendő alakítsuk át a pályát kvázi-egyenessé. Gondolatban rakjuk össze 10 km hosszú egyenes szakaszokból. Egy-egy szakasz 0,1°-ban hajlik el az előzőtől és közepe 2 méterrel tér el a körívtől. Megállapíthatjuk, hogy a különbség a kétféle pálya között az óra szempontjából gyakorlatilag nulla. Ugyanerre a következtetésre jutunk az ismert mechanikai törvény alapján is. A mozgási energia kizárólag az aktuális sebesség nagyságától függ, és nem függ a pálya alakjától vagy a mozgás irányától.
Vegyük észre, hogy az eddigi gondolatmenet és levezetés nem relatív, hanem abszolút sebességeket használ. Ez ellentétes Hafele és sok más jeles személy [3] vélekedésével. Azonban nyilvánvaló, hogy e problémakörben illetve e számítási procedúrában nem lehet a sebességskálát önkényesen ide-oda tologatni. Ezért a Föld kerületi sebessége, valamint a repülőgép v1+v2 un. valódi sebessége és a referenciaóra sebessége nem relatív sebesség, hanem abszolút sebesség.
Az óraparadoxon körül összegyűlt, meglehetősen komplex jelenségek mögé egy igen egyszerű kozmológiai hátteret lehet felépíteni. Eszerint a Földet egy láthatatlan fizikai mező fogja körül, amely együtt mozog vele, de nem forog együtt vele. A felvázolt kép első látásra talán bizarr, de létezik rá kézenfekvő és szemléletes magyarázat. E mezőhöz viszonyítva állnak egy helyben a pólusok, és az ehhez viszonyított sebesség képezi a tárgyak (pl. az atomórák) tényleges sebességét. Ha egy pillanatra átváltunk a realitásról az absztrakcióra (a fizikáról a geometriára), akkor úgy mondhatjuk, hogy ez az együttmozgó mező jelenti az abszolút koordinátarendszert. Ez vélhetően lokális rendszer, és a többi égitestet más- és más lokális mezők ölelik körül és követik mozgásukban.
A Michelson - Gale kísérlet 1921-ben optikai módszerrel mutatta ki a Föld forgását. A használt műszer a Sagnac- féle forgótárcsás interferométer földhöz rögzített, óriás méretű változata volt, ahol a fénysugarakat egy földalatti tárna vágataiban vezették körbe. Ily módon egy nagy alapterületű tárcsa alakult ki, melynek nagy mérete ellensúlyozta a Föld rendkívül kicsiny (1 fordulat/nap) forgási sebességét.

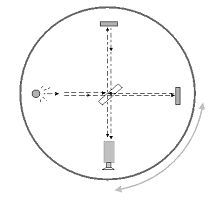
A kísérlet alapelvét illetve előzményét a Sagnac-féle kísérlet (1911) szolgáltatta. Ennél egy forgó tárcsa peremére rögzített tükrök terelik körbe a fénysugarakat. Mialatt a megosztott fénysugár két ága ellentett irányban körbefut a peremen, addig a félúton lévő egyesítő lemezke is arrébb mozdul néhány tized mikrométert. Ezáltal megváltozik a fényutak hossza, ami megváltozott interferencia-képet eredményez. Ebből visszaszámolható a tárcsa forgási sebessége, ami jó egyezést mutat a mechanikai úton mért értékkel. Hasonló jó egyezést mutatkozott az M-G kísérlet esetében is.
Az M-G kísérlet alátámasztja, továbbá kiegészíti a H-K kísérlet következtetéseit. Egyrészt megerősíti az együttmozgó fizikai mezőben forgó Föld teóriáját. Másrészt rámutat a mezőnek egy további meglepő tulajdonságára, hogy lenyúl a bánya mélyére, és odalent is ez határozza meg a fény sebességét, nem pedig a Föld forgó anyaga. Még inkább triviális e következtetés a Föld felszínén elvégzett Sagnac kísérletekre. Látjuk tehát, hogy hiába forog a Föld hiába forgatja a tárcsát a fizikus, a fénysugár nem kezd el forogni, illetve a legkisebb mértékben sem változtatja meg sebességét a forgótárcsa közelében. Logikátlan, sőt felelőtlen próbálkozás tehát, amikor egyes teoretikusok az SR és GR alapján nyert hibás választ megpróbálják feljavítani a Sagnac effektus beemelésével.
Az együttmozgó mező modelljét alátámasztja Michelson és Moorley interferométeres kísérletének (1887) negatív eredménye is. Az atomóra kísérlet megmutatta, hogy a fénysugár sebessége az együttmozgó mezőhöz viszonyítva állandó, nem pedig az un. állócsillagok rendszeréhez képest, ahogyan azt az M-M kísérlet idején gondolták. Ennek következménye, hogy nem jelent meg a laboratóriumi asztalra lehelyezett műszerben a Föld keringési sebessége. Elvileg megjelent ugyan a Föld kerületi sebesség, de két nagyságrenddel kisebb lévén a műszer ezt nem tudta kijelezni. Megállapíthatjuk, hogy a H-K kísérlet - bár némi bizonytalanságot még hordoz magában - igen eredményes volt. Igazolta, hogy a sebesség hatására az atomóra valóban késik. Egyben rámutatott a földfelszín rejtőző sebességére és ennek fontosságára. Ennek köszönhetően kerülhet vissza a fizikába az abszolút sebesség, és kerülhet a perifériára ellentettje, az érdemtelenül favorizált relatív sebesség. Végül ennek hátteréből bukkant fel egy új entitás, az együttmozgó fizikai mező. Ez várhatóan rendkívül jelentős hatással lesz a holnap fizikai és kozmológiai világképére.
Megjegyzések, irodalomjegyzék, táblázatok:
|
Table 1 Data of H-K experiment |
|||
|
|
Eastward |
Westward |
|
|
Time flight: |
41,2 hours |
48,6 hours |
|
|
Time total: |
65,4 hours |
80,3 hours |
|
|
Height: |
8900 m |
9400 m |
|
|
Recorded data: |
125 ** |
108 ** |
|
|
Time gain: |
-59 ± 10 |
+273 ± 21 |
|
|
Length of rout: |
34000000 * |
36000000 * |
|
|
Westward jurney: Washington D.C. - Dulles - Los Angeles - Honolulu - Guam - Okinawa - Hong Kong - Bangkok - Bombay - Tel Aviv - Athens - Rome - Shannon - Boston - Dulles - (Washington D.C.) |
|||
|
Washington D.C. :latitude: 37.5° * |
|||
|
Remarks: * estimated, ** unpublished |
|||
|
Table 2 Hafele's predicted [ns] |
||
|
|
Eastward |
Westward |
|
Gravitational: |
+144 ±14 |
+179 ±18 |
|
Kinematic: |
-184 ±18 |
+ 96 ±10 |
|
Net effect: |
-40 ±23 |
+275 ±21 |
|
Table 3 Predictions of formula (11) & (12) |
||||
|
Using formula (11): |
||||
|
|
Eastward |
Westward |
||
|
Time gain grav: |
+144 |
+180 |
||
|
Latitude of rout: |
37.2° |
31.0° |
||
|
Time gain kin: |
-184 |
+96 |
||
|
SUM Tgrav+Tkin |
-40 |
+276 |
||
|
Using formula (12): |
||||
|
Time gain grav: |
+144 |
+180 |
||
|
Time gain kin: |
-183 |
+118 |
||
|
SUM: |
-39 |
+297 |
||
|
Mistake % : |
-2 |
+8 |
||
[*] A konkrét kísérletekben annyi atomórát kell használni, hogy a mérési átlag a megkívánt hibahatáron belül legyen. Az egyszerűbb fogalmazás érdekében azonban a továbbiakban az "egy óra" kifejezést fogom használni.
[**] A jobb összehasonlíthatóság érdekében igyekeztünk megtartani Hafele jelöléseit és formulájának stílusát.
[1] Science 1972 177, 166-168 J.C. Hafele and R.E. Keating: Atomic Clocks: Predicted Relativistic Time Gains
[2] Science 1972 177, 168-170 J.C. Hafele and R.E. Keating: Atomic Clocks: Observed Relativistic Time Gains
[3] NATURE VOL. 238 p.244 AUGUST 4 1972 NEWS AND VIEWS Leader W.B.: Atomic Clocks Coming and Going
Keresőszavak: óra, pardoxon, Einstein, idődilatáció, relatív, sebesség, atomóra, Hafele, Keat
Kihelyezés dátuma: 2008
Formai és elvi módosítások: 2008 - 2021
Lektorálva: 2021.12.01.
Tassi Tamás
Gépészmérnök
Hobbi fizikus
Tud.és Szak. Író
www.aparadox.hupont.hu
*** Megjegyzés:
Friss információk tükrében a dolgozatban jelentős elvi módosítás szükséges. Lényege, hogy a kiegészítő kísérletekben az atomórákat egy km magas póznákra kell felhelyezni! A javasolt kísérletek így már nem elegánsak, de sajnos az éterszél csak a magasban fúj, talajszinten nem. Lásd: Éterszél kísérletek
Tt 2015.08.
*** Megjegyzés 2:
Egy viszonylag olcsó kísérlet könnyű és egyértelmű eredményt igér. Csörlő segítségével 10 km hosszú kötélen engedjünk fel egy meteorológiai ballont, rajta egy atomórával, egy napra. Odafönt már biztosan fúj az éterszél, Budapest fölött kb hangsebességgel, 340 m/s. Az óra késése 1 nap alatt: Dt=v2/2c2*T ~ 55 ns
Tt 2016 okt.
További adalékok a fenti témához
A cikk átdolgozott, jelentős változásokat tartalmazó változata megtalálható Globalizált paradoxonok néven. A link egy nyomtatható JPG formátumú verzióra mutat.



1. oldal 2. oldal 3. oldal
Honlapkészítés ingyen:
Ez a weblapszerkesztő alkalmas
ingyen weboldal,
ingyen honlap készítés...
Mai: 16
Tegnapi: 25
Heti: 16
Havi: 41
Össz.: 156 823
Látogatottság növelés
Óraparadoxon - © 2008 - 2026 - ora-paradoxon.hupont.hu