Óraparadoxon

A SPIN,  avagy  AZ ELEKTRON PÖRÖG!

Igen, az elektron valóban pörög!  Ezt így tartja a tudomány, minden kétség kizárt.  Ha ez így van, akkor kézenfekvő feltételezni, hogy a kis golyó a saját tengelye körül pörög.  A fizikusok is ezt feltételezték, mindjárt a kezdetekben.  Azonban szinte rögtön rájöttek, hogy ez nem lehetséges.  A pörgés túl erős, a golyó mérete túl kicsi.  A fénysebesség cca. 100-szorosára lenne szükség  a kerületen, ez pedig kizárt.   Az egyszerű, de nyilvánvalóan hibás N^o.1 elméletet sajnos rövid úton el kellett vetni. Mivel azóta sem született újabb elmélet, ezért a fizikusoknak fogalmuk sincs róla, hogy mit is takar ez a rejtélyes pörgés.  A következőkben bemutatom a N^o.2 elméletet, a sajátomat.  A neve CsMH.  A fentiek után nem lesz meglepő, hogy ennek ismertetéséhez elég mélyre kell merülnünk az előzményekbe és a részletekbe. 

Az elektron a legkorábban felfedezett elemi részecske.  Az 1800-as évek végén már javában kísérleteztek vele.  Az elektronok keresztülrepültek a légritkított üvegcsövön a katód felszínéről indulva (negatív töltésű fémlap), és a nagyfeszültségű anódlemezbe csapódtak.  A galvanométer pedig mutatta, hogy az üvegcsőben tényleg áram folyik.  Ha a légritkítás rossz minőségű volt, akkor a cső világított, és az áramot döntően az elektronok által ionizált gázmolekulák vezették.  Keresztirányú elektromos és mágneses tér hatására az elektronok pályája meggörbült, mégpedig töltésük és tömegük arányában.  

Hát így indult az elektron karrierje.  Ma már ő ül a trónon, az ipar az informatika, a számítástechnika alfája és ómegája.  Mi most mégis az elektron alapvető és ez ideig ismeretlen tulajdonságait próbáljuk a továbbiakban feltárni. 

     A tudomány számos kísérlet útján nagy pontossággal határozta meg az elektron alapvető paramétereit.  A legújabb kutatások szerint az alakja valószínűleg szögletes, de az egyszerűség érdekében tekintsük kis golyónak.  Ennek mérete egy régebbi becslés szerint 2,8*10^-15 méter.  Tömege igen kicsi, (910*10^-33 kg), ámde töltése ehhez mérten nagy (160*10^-21 coulomb.) 

    Végül van az elektronnak un. elektromágneses momentuma, szakszóval szpinje.  A mai, un. "modern" fizikusok szerint ennek értéke 1/2.  (?) E szám (?) valamiféle forgást, pörgést takar. Csak két irányba mutathat, fel és le. E dolgozat célja megkísérelni a lehetetlent, és valamiféle egyszerű, szemléletes, sőt, koherens magyarázattal szolgálni az 1/2 feloldására, illetve a szpin mibenlétére. 

     Kezdjük a dolgok kibogozását egy évszázada ismert kutatási eredménnyel.  E szerint nem csak az elektron pörög, hanem az összes többi szubatomi részecske is. Akár kicsi a részecske, akár nagy, akár könnyű, akár nehéz (neutrínó, proton, neutron, Z bozon stb.), a szpinje mindegyiknek a már említett 1/2 értékű.  Ez az egyhangúság számunkra nem a kiút elrejtését jelenti, hanem ellenkezőleg, a legjobb segítséget adja. Ebből ugyanis rájöhetünk, hogy nem a részecske szabja meg azt, hogy mennyi legyen a szpinje, hanem valami láthatatlan közeg, ami ott rejtőzik a háttérben.  Ez az un. éter, melynek igen erőteljes elektromos és mágneses tulajdonságai vannak.  Mivel a részecskék között elektromosan semlegesek is akadnak, ezért bizonyára a mágneses hatás a meghatározó.  E hatások makroszkopikus testek vonatkozásában kiátlagolódnak.  Ne csodálkozzunk hát, ha mi nem érzékeljük sem az étert, sem annak furcsa hajlamát, hogy pörgetni akarja a bele merült testeket.   Persze a szubatomi részecske önerejéből nem is lenne képes pörögni.  Az éter az, ami kényszeríti erre.  Sőt, az éter a pörgést folytonosan pótolja, hiszen a részecske folytonosan veszít belőle. A veszteség oka lehet ütközés, vagy elektromágneses sugárzás.  Fontos tehát leszögeznünk, hogy a pörgés, azaz a szpin alapvető forrása az éter.  A részecskék csak elszenvedik és megjelenítik az éter e bizonyos rejtett, ámde igen erőteljes és extrém tulajdonságát. 

De Broglie (ejtsd: dö Brozsli) francia amatőr fizikus tette meg az első lépést a szpin felderítésének útján.  Az Ő elméjében fogant meg az a gondolat, az elképesztő ötlet, hogy az elektron részecske is és hullám is.  Hol részecske, hol hullám, a környezet hatásaitól illetve a megfigyelési technikától függően.  Avagy mindkettő egyszerre, egyazon időben?  Miért is ne, ha a fény elismerten kettős természetű, azaz részecske is, és hullám is? 

     De Broglie elküldte dolgozatát Einsteinnek, mint közismerten merész gondolkodású, haladó szellemű tudósnak.  Annak, aki a legnagyobb lépést tette meg a fény kettős természetének útján.  Ő beleolvasott, majd rövid úton a szemétbe dobta.  Mentségére szóljon, hogy néhány hónap múlva előhalászta.  Szerencsére nagy szemétkosarai voltak, amiket szinte sose ürített.   Újra elolvasta, és újra elvetette.  Mindazonáltal mégiscsak továbbküldte néhány vezető fizikusnak, egy pozitívnak nem-igen nevezhető ajánlással: "Ez egy őrült elme ötlete, de kétségtelenül van benne ráció!"  Az őrült gondolatot később kísérlettel is vizsgálta Brag és Brag (ejtsd: Breg- Apa és fia), és láss csodát, igazolták a sejtést!  Az ezüstatomok kristályrácsán átrepülő elektronok interferencia-mintázatot mutattak.  Azaz a repülő elektronok hullámként viselkedtek. 

De Broglie később egyéb ötletekkel is próbálkozott.  Fagolyókból atommodelleket készített, melyeket azután ide-oda elküldött.  Ennek az esetnek magyar vonatkozása is van.  Nyilván megtudta, hogy a Budapesti Műegyetem professzora, Novobátzky Károly nagy Einstein rajongó. A Frankhonból érkezett szállítmány ott kuncsorgott a Műegyetem főépülete előtt, de Novobátzky professzor még a kapun sem engedte bejönni.  "Ez a felfuvalkodott hólyag azt képzelte, hogy éppen ő oldja meg az atom rejtélyét!  De én móresre tanítottam!" – írta később büszkén.  Novobátzkynak nyilván antipatikus volt de Broglie, a hobby-tudós. (Nekem viszont ellenkezőleg!  A kedvenc fizikusaim között van.)

A szubatomi részecskék egytől-egyig kettős természetűek – ma már így szól a tétel.  E tétel mögött semmi valóságos modell nem áll. A fizikusok rég beletörődtek, megszokták, sőt, elhitették, hogy a szubatomi részecskék világában minden - de minden más logika mentén, és valójában másképpen történik, mint a makro-világban.  Ezért szerintük ott minden mozgás illetve jelenség "virtuális",  a köznapi logika számára megjeleníthetetlen és "abnormális".  Jelenleg tehát ezen a szinten állunk, és innen kell feljebb lépnünk a szemléletesség irányába. Illetve azért, hogy jobban közelítsük a fizikai valóságot, az emberi szemléletet illetve a tapasztalati eredményeket.

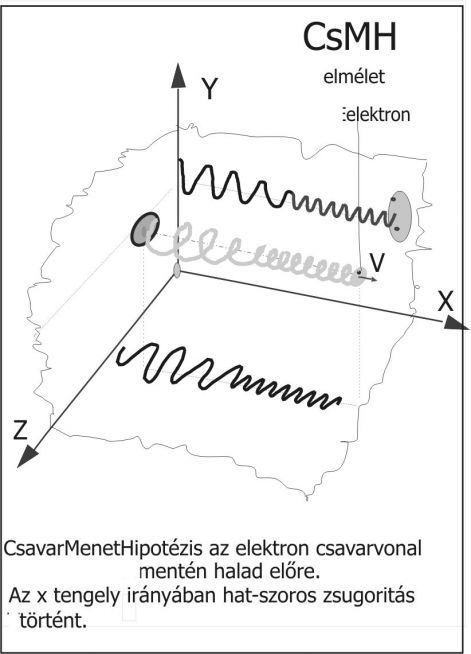
     Tegyük fel, hogy az elektron nem más és nem több, mint egy szimpla szubatomi  részecske, egy golyócska, ami viszont haladás közben hullámmozgást is végez.  Ezen túlmenően azonban a hullámmozgás fogalmát is bővítenünk kell.  Amikor ugyanis hullámot mondunk, akkor többnyire oldalról nézett síkbeli hullámra gondolunk.  Témánknál maradva tehát az elektron halad és közben valamilyen síkban hullámzik is.  Például fel-le mozog.  Az így befutott síkbeli pályát a matematika szinusz-görbének nevezi.  Az egyszerűsített – mondhatnánk korcs – síkbeli pálya valójában egy térbeli mozgás vetülete.  Az elektron minden bizonnyal térbeli pályán mozog, éspedig csavarvonal mentén. (A csavarvonal nemzetközi neve helix.) Könnyű modellezni: Lágy drótot kell csavarni egy hengerre, mégpedig nagy menetemelkedéssel.  A drót mutatja a befutott pályát, míg a végére szúrt kenyérgalacsin jelképezi magát az elektront. Kétféle csavarmenetet tudunk készíteni.  Jobbra csavarodót, azaz jobb-menetűt, vagy balra csavarodót, tehát balmenetűt.   E kétféle csavar sehogy se illik egymásba, bárhogyan is forgatjuk őket.  Valójában csak kétféle csavarmenet és kétféle szpin létezik: Jobbos és balos.  Ez úgy értendő, hogy a térbeli görbe a haladás irányához képest jobbra illetve balra csavarodik. 

      A mágneses momentum kétféle formájának jelenleg használatos jelölése – fel és le nyilak – zavaró, sőt, félrevezető.  Közismert, hogy az űrben nincs kitüntetett irány, tehát nincs fent és lent sem.  Ráadásul ezek a nyilak tökéletesen fedésbe, azonos állapotba hozhatók 180 fokos elforgatás útján. A fő probléma mégis az, hogy a tudományos világ kvázi elfogadta. Képességeiket meghaladja egy magasabb szintű geometria kifejlesztése, illetve keresgélése. Persze, igen kényelmes a részecskék mellé nyilacskákat rajzolni.  Miért nem tűnt fel a fizikusoknak, hogy a fel és le nyilak nem érnek fel a nekik tulajdonított fizikai tartalom szintjére.  Azért, mert a fizikusok nem tanulnak geometriát.  Bólogatnak a fel-le nyilakra – mint Pistike a hátsó padsorban – és pesze eszük ágában sincs magasabb szintre lépni. 

      A jobb-balcsavar tökéletesen lefedi a kétféle szpin jelenségét. Ez komoly alátámasztása a korábban említett CsMH-nak, azaz a Csavar Menet Hipotézisnek. Valójában ez maga a CsMH, bár nyílván bővebb mgyarázatot igényel. 

A CsMH-nak sajnos számos bizarr eleme van, de ez a szubatomi részecskék világában már megszokott, sőt, szinte elvárt.  Itt például megjelenik a kiegyensúlyozatlan tömeg jeélensége, az elektron keringő mozgása közben.  Egy golyó, spárgára kötve, de a spárga másik végéről hiányzik a kéz, ami ellen-tart a centrifugális erőnek.  Akad más példa is ilyen "lehetetlen" esetre?  Igen, többet is találhatunk.  Ilyenek a Föld mágneses terébe beérkező töltött részecskék, többnyire a napszél protonjai és elektronjai. Ezek csavarvonal pályán köröznek a van Allen övben, miközben nagy sebességgel haladnak a pólusok felé. Sok elektromos eszközben és mérőműszerben lép fel hasonló effektus. Láthatatlan mágneses erővonalak tartják meg körpályán a részecskét.  Maga a mozgó töltés is mágneses teret kelt maga körül, így az elektron tulajdonképpen a saját mágneses terében mozog.  A vákuum roppant erős mágneses permeabilitással rendelkezik, ami az itt szereplő nagyon kicsiny távon igen nagy visszatérítő erő kifejtésére lehet képes. (További extrém lehetőségek ismertetését itt most mellőzöm.)

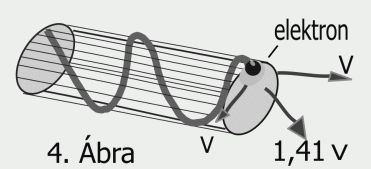
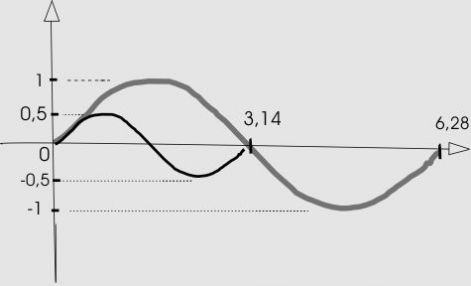
  Az elektron térbeli pályáját a következő módon szerkeszthetjük meg.  Felrajzolunk egy r sugarú kört, majd a középpontjából, rá merőlegesen indítjuk a mozgás haladási irányát jelölő vektort.  A golyócska – az elektron – a körön kering, miközben előre is halad.  Mindkét mozgás szigorúan egyazon v sebességgel történik.  A kör kerülete 6,28r.  Ez alatt az elektron ugyanennyit, azaz 6,28r távolságot halad előre.  Ez egy meredek emelkedésű térbeli csavarvonalat eredményez, melynek emelkedési szöge pontosan 45 fok.  Az elektron tehát v sebességgel kering, és ugyancsak v sebességgel halad előre.  Ez két, egymásra merőleges sebesség. Térbeli összegük 1,41v. Az elektronnak tehát valójában nagyobb sebessége van, mint amit a műszerek mutatnak.

Függ-e a csavarvonal alakja és mérete a haladási sebességtől?  A kinézete mindig arányos marad, míg a mérete fordított arányban változik.  Ha kétszer nagyobb lesz a sebesség, akkor kétszer kisebb lesz a kör sugara, és persze kétszer kisebb lesz a menet emelkedése is.  A 45 fokos emelkedési szög tehát változatlan marad. Ugyanakkor az elektron a kétszeres sebességgel kétszer hosszabb utat fut be.  Erre az útszakaszra tehát 4 darab kisebb csavarmenet jut.  Ez a furcsaság - mint látni fogjuk - a szpinértékének állandóságából következik. 

      Valószínű, hogy a szpin valójában az elektron impulzus-nyomatéka.  Ez a mechanikai mennyiség az m tömeg, a v sebesség és a körmozgás r sugarának szorzata. Azaz szpin=m*v*r.  A mértékegységek rendre: kg*m*m/s.  A szokásos összevonással - és így már alig látszik az értelme és eredete - [kgm²/s]. A szpin értéke valójában 53*10^-36 [kgm²/s].  A fizikusok által oly sűrűn emlegetett 1/2-et a továbbiakban tekintsük afféle fedőnévnek, esetleg jelképnek, de mindenképpen pongyola fogalmazásnak.

Az impulzus-nyomaték szerepét az égi-mechanikában lehet egyszerű példákkal bemutatni. Két égitest kölcsönhatását vizsgálva, szinte ez az egyetlen megmaradó mennyiség.  A Nap körül keringő Földre ennek értéke 26*10³⁹ [kgm²/s], ami számunkra nagynak tűnik, bár a Jupiterhez képest elhanyagolhatóan kicsiny. Miközben a Föld járja ellipszispályáját, közben a sebessége és naptávolsága, sőt elméletileg a tömege is folyton változik.  A biztos pont az impulzus-momentuma, ami viszont szigorúan megmaradó mennyiség. 

     Az elektron impulzus-momentuma szpin=53*10^-36, ami nekünk, embereknek roppant kicsinek tűnik.  A méretéhez és a tömegéhez mérten viszont roppant nagy.  Olyannyira nagy, hogy amint azt fentebb láttuk, egyszerűen nem fér bele.  Az impulzus-momentumát tehát rajta kívül, az elektront körülvevő térben kell keresnünk.  Lám, sikerült is ott megtalálnunk! 

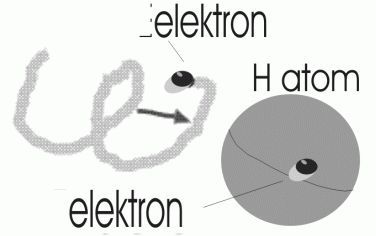
Most nézzünk meg egy konkrét csavarmenetet.  Ennek méretei az elektron sebességétől függnek, ami viszont bármennyi lehet.  Legyen a v a fénysebesség 0,36%-a, ami egyben a hidrogénatom 1.  pályáján keringő elektron sebességének fele, ha a Bhor-féle atommodell szerint számolunk.  Ekkor r értéke 53piko-méternek, azaz 53*10^-12 adódik. (A hasonlóság a szpin számértékéhez puszta véletlen.)  Ez az r érték a hidrogénatom elektron-pályájának sugarával azonos. Ahogyan az ábra mutatja, a csavarmenet-pályán érkező elektron éppen érinteni fogja a gömb alakú hidrogénatomot. 

      Ha az atomnak véletlenül nincsen elektronja, akkor az érkező elektron geometriai paramétere éppen megfelelő lévén, jól pályára tud állni.  A köröző mozgás átalakul atomi pályamozgássá.  De mi lesz a haladó mozgással?  Nem vész el, és nem sugárzódik szét energia formájában!  Rejtőzve bár, de benne marad az atomban.  Talán ez segíti az elektront, hogy az eddig hengerre tekeredett csavarmenet most rátekeredjen a gömbfelületre.   Tehát ne csak egy gyűrű mentén keringjen, hanem bejárja az egész felületet.  Erre a különleges produkcióra semminemű megoldása nincs az eddig megalkotott atommodelleknek.  Megjegyzem, hogy Jómagam is 4 évtizede keresem a megoldást – eredménytelenül. (Valószínűsítem, hogy a megoldás a 4. dimenzióban van.)  Azonban a helyzetet nem tartom kilátástalannak. Reménykedem abban, hogy akad valaki, aki végre rábukkan a dolog nyitjára. 

   A mag és az elektron közötti vonzóerő az egyetlen jól követhető erőhatás.  Ennek értéke hidrogénatom esetén 82 nano-newton.  Ezt a jelentékeny erőhatást bizony be kellene iktatnunk az eddigi geometriai levezetésbe – csak az a baj, hogy nem hagyja magát beiktatni.  Maga Niles Bhor viszont atommodellje megalkotásakor (1913) kizárólag ezzel az erővel dolgozott, a szpin akkoriban még teljesen ismeretlen fogalom volt. Kétszeres pályasebességet kapott, és posztulálta (önkényesen feltételezte), hogy a pálya kerülete a Planck állandó egész számú többszöröse.  Esetünkben – a legbelső pályán – n=1, azaz a legkisebb egész szám.  Az eddigi geometriai megfontolás is n=1 értéket adott, hiszen 1 csavarmenet feküdt rá a gömbfelületre. 

     Valójában mindkét szempontot egyesíteni kellene a hidrogénatom modelljében. Sőt biztosan jelen van ott a mágneses erőtér is, és nagy valószínűséggel egyéb feltáratlan kölcsönhatások előterei is. Mindez arra utal, hogy a megoldásra csak a távoli jövőben van remény.

   Az atomban az elektronoknak többnyire kétféle momentumuk van. Egy un. pálya-momentum, továbbá a szpinjük. Úgy vélhetnőnk, hogy a példában szereplő hidrogénatom héja kétféle szpinnel fog rendelkezni.  Egy, amit a beérkező elektron hozott, és egy másik, amit az atom pálya-momentuma képvisel.  A helyzet ezzel szemben az, hogy a hidrogénatom héjának csak egyetlen momentuma van. Ez pedig nem a pálya momentuma, hanem az elektron szpinje.  A hivatalos tudomány legalábbis ezt állítja. 

       Mindezekből több következtetést is levonhatunk:

1.  A szpin jóval alapvetőbb, elemibb fogalom illetve fizikai tényező, mint az atom.  

2.  Elsőnek tehát a szpint kell megértenünk.

3.  Az atomok elektronhéja valószínűleg nem fér bele az általunk ismert 3 dimenzióba.  Ennél többet – például 9 dimenziót – pedig csak matematikával tudnánk lekezelni.  Az értelmünket, a 3-nál több dimenzió meghaladja. 

   Evezzünk most vissza az atom modellezésének viharos tengeréről viszonylag nyugodtabb vizekre, vissza a szpinhez.  Ott még találunk jó pár érdekességet vagy magyarázatra szoruló tüneményt. 

  Mint tudjuk, az elektronok szabadon kószálnak a vákuumban, a levegőben és a fémekben.  Ezen közben időről-időre útjukba esik egy-egy atom.  Ennek elektronburkán akadálytalanul átrepülnek, mert közel nulla az esélye annak, hogy két kicsiny golyócska éppen összeütközzön.  Különben is taszítják egymást.  Az atommag azonban egészen más eset.  Ellentétes töltésével maga felé vonzza, mintegy beszippantani próbálja a kószáló elektront.  Az akció sikeresnek indul, az intenzív erőtér hatására az elektron irányt vesz a mag középpontja felé.  Közben az elektromos erőtér hatására gyorsul is, ami a csavarvonal torok-körének – r sugarának – csökkenésével jár, de nem csökken eleget.  Mostani példánkban az elektron a fénysebesség 0,36%-ával halad, és éppen érinti az atom burkát.  10-szer nagyobb sebesség csak 10-szer kisebb torok-kört eredményez, miközben a mag viszont kb.  10000-szer kisebb.  Az elektron elméleti útvonala ugyan áthalad az atommagon, de ezen közben ő maga csavarvonal mentén haladva viszonylag széles ívben kikerüli azt. 

Nagy baj lenne, ha a kóbor elektronok folyton belerohannának az őket vonzó atommagokba.   Ketté hasítanák a magot, vagy egy protonnal egyesülve neutront és ezzel rendszám-csökkenést váltanának ki.  Ilyen események azonban spontán módon nem történnek. Ez kész csoda! – mondhatjuk alapszinten állva.

Az atomfizikusok máshogyan magyarázzák a csodát, az ütközés hiányát:  " Mert csak! "  Ennél jóval mélyebb magyarázattal szolgál a CsMH elmélet.  E szerint tehát az elektron elméleti középvonala igen is átmegy a magon, de eközben maga az elektron csavarvonal mentén elkerüli.  Ez tehát a 2.  érv,  amely alátámasztja  CsMH  teóriát. 

      A rend kedvéért el kell mondanunk, hogy a fénysebességet nagyon megközelítő elektronok képesek eltalálni az atommagot, a protont, sőt akár a bennük száguldozó 3 kvarkot is.  Ezt egy további rejtélyes jelenség teszi lehetővé, mely szerint a tömeg c-t közelítve rohamosan nő, mégpedig a jól működő Lorentz-képlet szerint.  Szó nincs arról, hogy ez virtuális, elvont jelenség lenne.  Ilyenkor a tömeg ténylegesen növekszik, esetenként drámai mértékben.  Így az elektron sebességét egy gyorsítóban egyre fokozva, a tömege sok nagyságrenddel megnőhet.  A szpin=m*v*r egyenlet alapján az m növekedésével az r, a csavarmenet torok-köre fog nagyságrendekkel csökkenni.  A csökkenésnek  nincs alsó határa. 

Tassi Tamás 

aparadox.hupont.hu

Ez a cikk a TUDOMÁNY MÁGIÁI című könyv II. kötet (2010) alapján készült

Az, hogy weboldal ingyen annyit jelent, hogy minden ingyenes és korlátlan: weboldal ingyen.

ÁSZF | Adatvédelmi Nyilatkozat